导数要看做某一点附近的变化率,而不是某一点的瞬时变化率,因为瞬时没有意义
- 瞬时是啥,能吃吗? #### 导数完全体 \[ \frac{ds}{dt}(t)=\frac{s(t+dt)-s(t)}{dt} \]
符号\(d\)表明了就是要求\(d\)描述的值趋近于0时的结果
- \(dt\)表明\(t\)趋近于零
- 导数的本质并不是分数,而是当所求变化量越来越小时这个比值的极限
求一个函数\(s(t)=t^3\)在\(t=2\)时的导数
- 先写出导数完全体
\[ \frac{ds}{dt}(2)=\frac{s(2+dt)-s(2)}{dt} \]
\(\frac{ds}{dt}(2)\)可表示为\(\frac{d(2^3)}{dt}\)
再转换
\[ \frac{ds}{dt}(2)=\frac{(2+dt)^3-(2)^3}{dt} \]
- 分步乘法
\[ \frac{ds}{dt}(2)=\frac{2^3+3(2)^2dt+3(2)(dt)^2+(dt)^3-2^3}{dt} \]
- 化简
\[ \frac{ds}{dt}(2)=3(2)^2+3(2)dt+(dt)^2 \]
- 因为\(dt\)趋近于零,所以任何数乘以\(0\)都得零
\[ \frac{ds}{dt}(2)=3(2)^2 \]
- 得到结果
\[ \frac{ds}{dt}(2)=12 \]
结论(学完微积分后的本能想法,不必从头推导)
\[ \frac{ds}{dt}(2)=3(t)^2 \]
基本的组合函数
加法法则
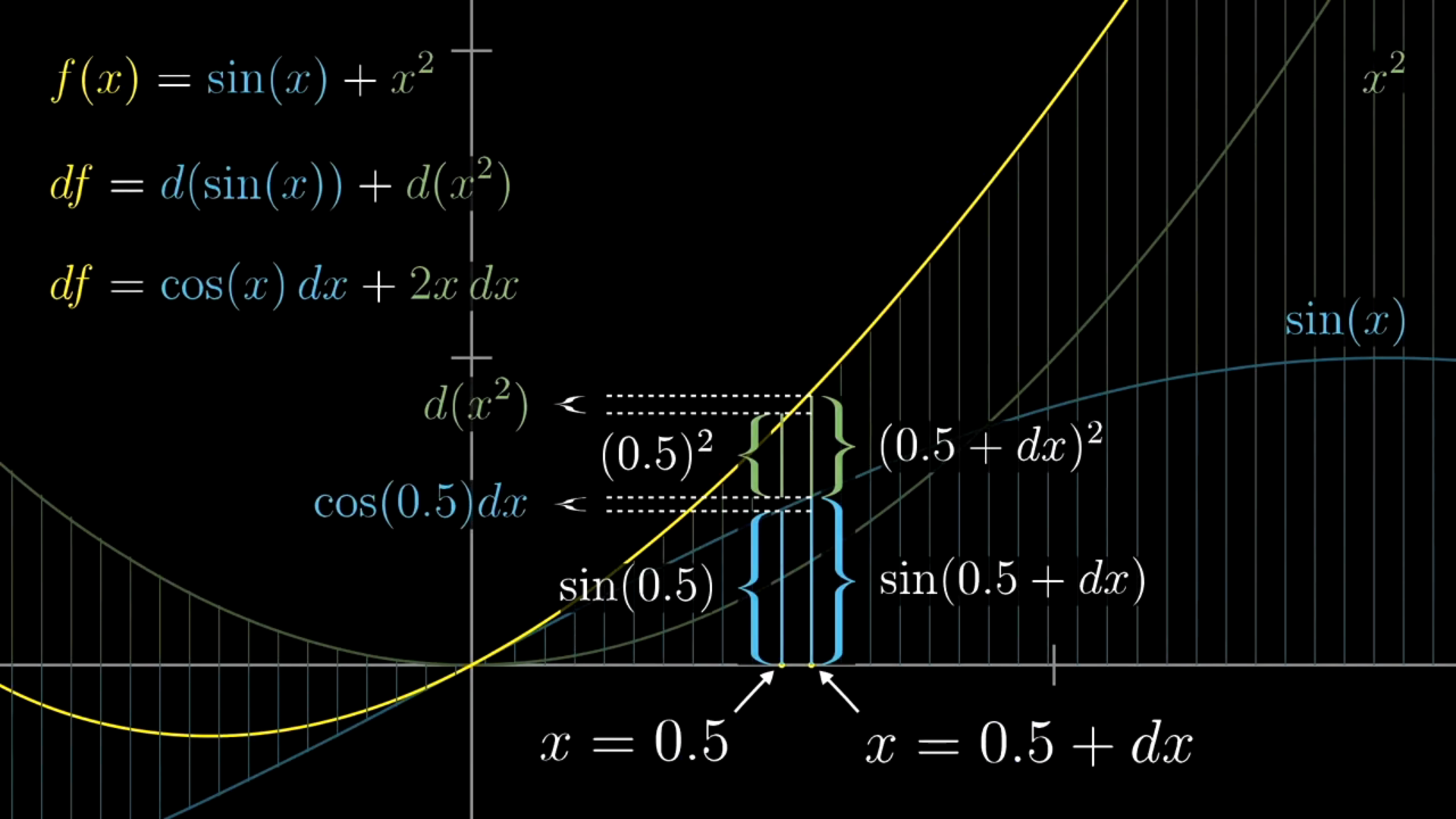
口诀:组合函数加法就是先对其中的元素进行求导,再相加

乘法法则
处理乘积通过面积来思考会更合适
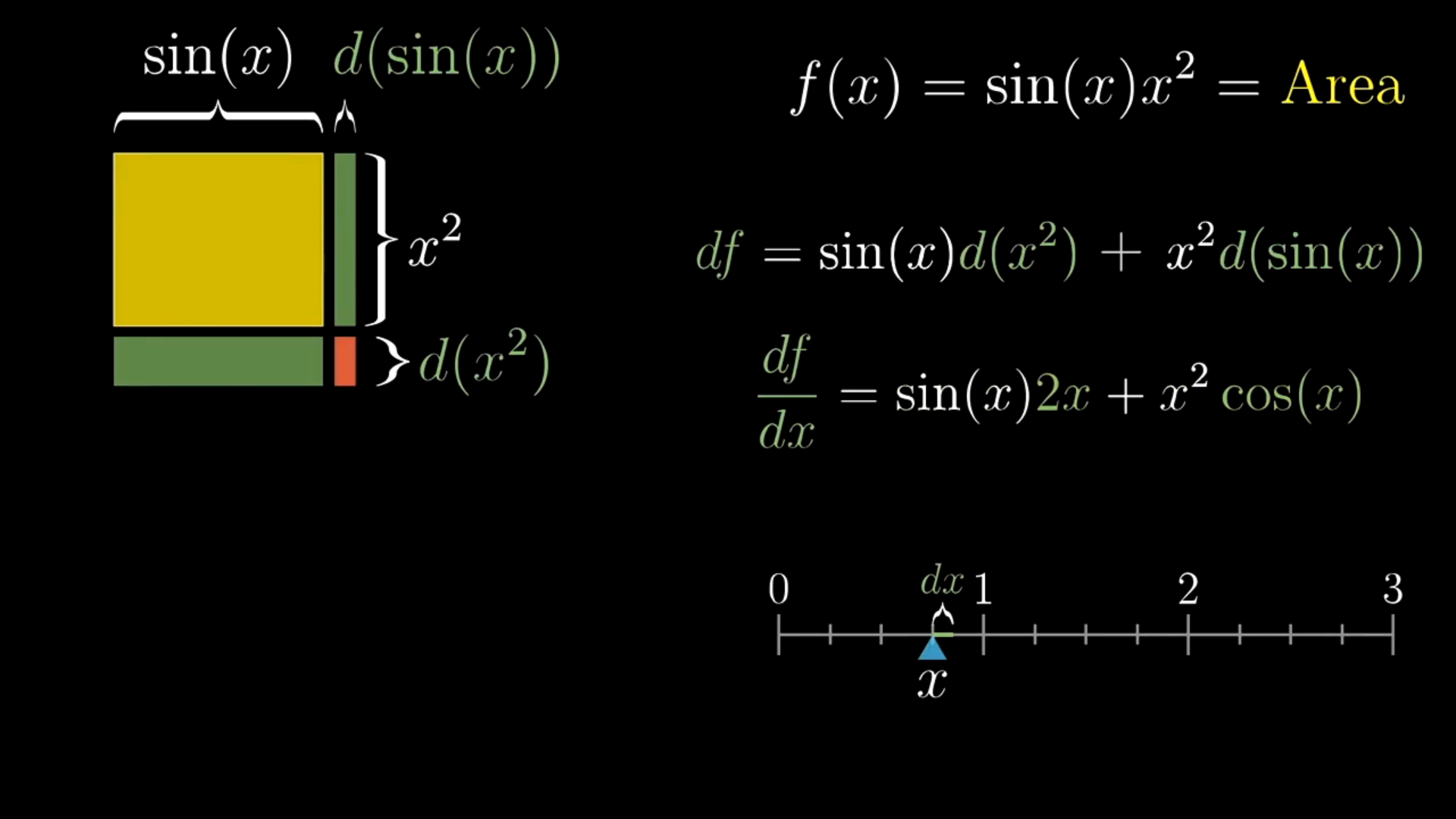
口诀:前导后不导,后导前不导
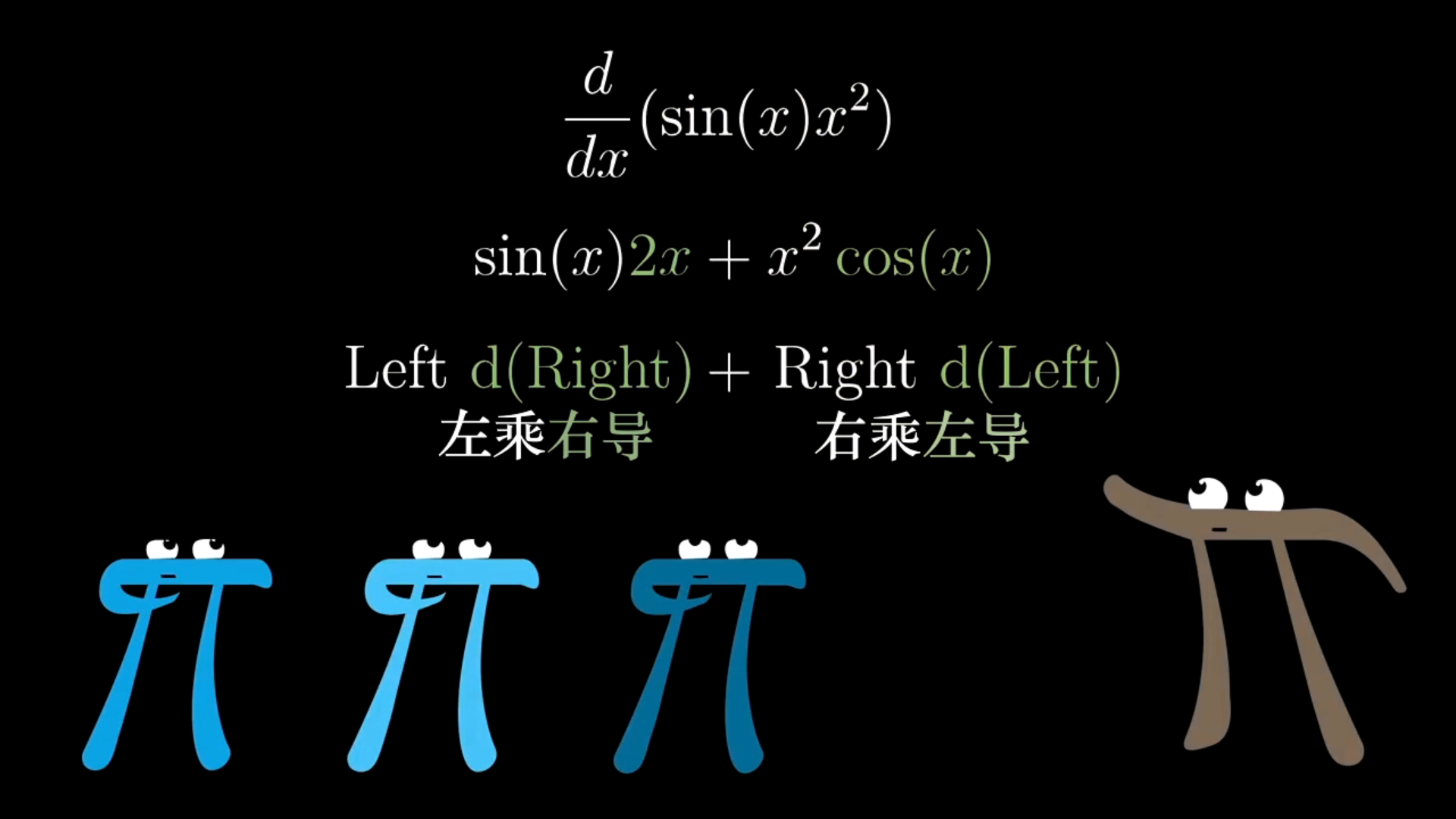
链式法则

多元复合函数求导法则
口诀:分段用乘, 分叉用加, 单路全导, 叉路偏导

